Making Floating Point Calculations Less Cursed When Accuracy Matters [Hackaday]

View Article on Hackaday

An unfortunate reality of trying to represent continuous real numbers in a fixed space (e.g. with a limited number of bits) is that this comes with an inevitable loss of both precision and accuracy. Although floating point arithmetic standards – like the commonly used IEEE 754 – seek to minimize this error, it’s inevitable that across the range of a floating point variable loss of precision occurs. This is what [exozy] demonstrates, by showing just how big the error can get when performing a simple division of the exponential of an input value by the original value. This results in an amazing error of over 10%, which leads to the question of how to best fix this.

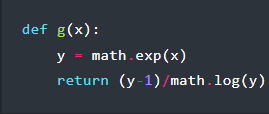
Obviously, if you have the option, you can simply increase the precision of the floating point variable, from 32-bit to 64- or even 256-bit, but this only gets you so far. The solution which [exozy] shows here involves using redundant computation by inverting the result of e^x. In a demonstration using Python code (which uses IEEE 754 double precision internally), this almost eradicates the error. Other than proving that floating point arithmetic is cursed, this also raises the question of why this works.

For the explanation some basic understanding of calculus is rather helpful, as [exozy] looks at the original function (f(x)) and the version with the logarithm added (g(x)). With an assumption made about the error  resulting with each arithmetic operation (δ), the two functions can be analyzed, adding a 1 + δ assumption following each of these operations and simplifying them as much as possible. For f(x) it becomes clear that it is the denominator which is the cause of the error, but we have to look at g(x) to make sense of what changes.

Intuitively, log(ex) helps because it somehow cancels out the error in ex, but what really happens is that with the small inputs used for x (g(1e-9), g(1e-12) and g(1e-15)) the approximations result in the simplified breakdown shown here (fl()). With a larger x, the Taylor series expansions used in the analysis no longer apply. What seemed like a fix no longer works, and we are left with the stark realization that representing real numbers in a fixed space will forever be the domain of tears and shattered dreams.